Lacanian structure of the subjective as consequence of the signification relation
by Tomasz Gil © 2012
Available in PDF version.
Abstract
The Lacanian premise that the human subject is a system of signifiers bound by a signification relation is treated with mathematical rigor and allows one to define subsets of signifiers that can be termed as Unconscious and Imagined. The properties of those subsets give rise to a certain structure of the subjective very closely resembling Lacanian insights. In particular a set functioning very much like a Lacanian Real can be identified. We define a foreclosed set and show that it can only be a subset of the Real. Also certain restrictions on how elements of the Real, Unconscious and Imagined can mutually relate correspond to key psychoanalytic ideas.
Introduction
In Lacan's view the human subject is constituted as a consequence of being introduced into the world of signifiers which lead him away from a simple reality of living. The subject invests his energies in protecting an image of himself - the ego - and into developing a persona defined by the rules of the world - the barred subject $. These are the regions that Lacan named Symbolic and Imaginary and their operation is the main characteristic of Lacanian subject. In addition to those Lacan also identifies a third realm - the Real - which corresponds to the core reality of living. The real is the "Thing" that is always in one place and, even though seemingly passive, it is the motivating center for the activities in the other realms - ostensibly as the locus of the lost object of primordial jouissance.
In this paper I consider the subject plainly as a system of signifiers and signifieds bound by a signification relation. I study the mathematical structures that can be identified in a system as a result of the signification relation. In short I take the Lacanian statement - "the subject is nothing but a result of the system of signifiers" - at face value, look for mathematical results that are rigorously reachable and interpret them in Lacanian terms. Mathematics is a system of formalization of intuitions that can be taken up by the intellect and be granted full membership in the domain of reason. The mathematics of this development is rigorous while their interpretation is tentative and to a degree speculative as no clinical data or insights are involved.
The mathematics of this paper is not the axiomatic set theory that certain philosophers would take as the basis for ontology. We are not studying ontology but information theory akin to the theory of relational databases. The core mathematical concept is that of relation which is a certain generalization of the concept of function.
The subjective space and the signification relation
Let Ω be a set of elements, also called items, constituting a space. We will provisionally consider this space to be the space of the subjective. Signifiers and signifieds are all equivalent elements of Ω.
Let us consider a binary relation Σ on set Ω meaning a subset of the Cartesian product of the space on itself. In other words this is a selection of ordered pairs (x,y) where x and y are elements of Ω
This is to say that certain pairs (x,y) belong to Σ.
where x ∈ Ω and y ∈ Ω
We will also say that x and y are in relation Σ and write simply
This will be the preferred notation for relation Σ. When in the relation pair x → y can be viewed as signifier and signified with these terms designating roles in the relation rather than characteristics of x and y taken separately. Also note that a given x can be in relation with more than one y and vice versa.
Relation Σ is to represent the significations in effect in the space of the subject. Relation Σ is taken at an instant in time as we consider a temporally fixed point in the history of the subject and attempt to study the subject's structure.
The meaning of the signification relation is the signifier-signified relationship where x is the signifier and y the signified. The relation Σ simply lists which items x denote which items y. To be clear, the term signifier and signified denotes merely the role of an item x ∈ Ω or y ∈ Ω in a given pair (x,y) and is not its characteristic. A more descriptive terminology would be name and image and we will use it to bring us closer to the intuitions we want to formalize. The objective of this paper is to study the structures that can be discerned in Ω as induced by the relation Σ.
Unconscious and imagined sets
Let us call any set U ⊂ Ω having the property
unconscious set. This set has the property of not having any element from outside of it point to any of its elements.
Furthermore let us call any set I ⊂ Ω having the property
imagined set. This set has the property of not having any element from outside of it pointed to by any of its elements.
It is easy to prove that a union of two or any number of unconscious sets is also an unconscious set. Likewise the union of any number of imagined sets is also an imagined set. This will be even easier to see after we introduce new definitions.
The global set Ω is both unconscious and imagined. Including Ω in the aforementioned unions leads to uninteresting triviality erasing all structure. Or perhaps it describes animal subjectivity.
Let us take subset A of Ω — A ⊂ Ω. Then we define:
and call it the signifieds of A, (s.t. = "such that"). Set M(A) will comprise all targets of significations of elements of A. We call them images of A. Further, we define:
and call it the signifiers of A. Set N(A) will comprise all origins of significations of elements of A. We call them quite intuitively names of A.
For single element set A = {x}, that is consisting only of element x, we can write:
The above says that M are all those elements pointed to by x, while N are those that point to x.
With help of the definitions of the M and N functions on the space of subsets A of Ω we can produce these characterizations of imagined and unconscious sets. Namely, for any unconscious set U:
and for any imagined set I:
It is easy to show that it is in fact so along with the inverse i.e.:
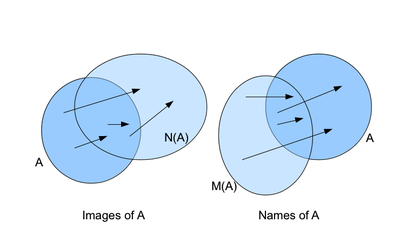
Figure A. Set A and its images M and names N. For an arbitrary set A there is no restriction on how it might overlap with its images and names. The arrows show examples of elements realizing the signification and the N and M set mappings. If set A is unconscious then N(A) would be completely contained in A. If A is imagined then M(A) would be completely enclosed in A.
The whole unconscious and the whole imagined
Since the union of any number of unconscious sets is an unconscious set we can construct the union of all such sets (except Ω itself). This will be called the whole unconscious - Υ0. Let us write:
where U are all proper (i.e. U ≠ Ω) unconscious sets. Likewise for the whole imagined set - Ι0:
where I denotes all proper imagined sets. The interesting cases will of course occur when the whole unconscious and the whole imagined do not fill the whole space, i.e.: Υ0 ≠ Ω and Ι0 ≠ Ω. The part of Ω outside of the whole unconscious and imagined subspace is the conscious part which is a characteristic of the human psyche. In psychoanalysis we are interested in the unconscious and imagined while the most available part of the psyche is of course the conscious part. This should not mislead anyone into presuming that consciousness it the main object of interest. As a matter of fact we have not defined the conscious space and will not have a need to do so. Let us observe that the unconscious and imagined space have been defined by demanding that they obey certain conditions. Anything outside of those spaces combined will not satisfy these conditions which will indicate that these elements are more accessible to observation and investigation, which usually follows a chain of signifiers, - aka appear as conscious elements.
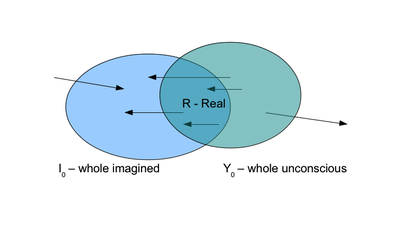
Figure B. Υ0 and Ι0 intersecting into R. The arrows again indicate possible significations. Note how they observe the restrictions imposed by the definitions of these sets: no arrow points into the unconscious from its outside, no arrow points out of the imagined outside of it.
Equations (10) and (11) obviously hold for the whole unconscious Υ0 and the whole imagined Ι0, respectively. However, we would like to consider sets defined by the M and N mappings acting on these sets.
I would like to call set P the poetic set and set S the symbolic set. In plain language set P is comprised of all the names for imagined items while S is comprised of all the images for unconscious signs/names. The elements of P are x s.t. x → y, where y ∈ Ι0 - which means is something that points directly to an imagined item. An element in S is x s.t. y → x where y ∈ Υ0. P and S are spaces near the edge of the imagined and unconscious, respectively. Regions of P and S may be outside of the unconscious and imagined and thus more empirically accessible. When they are the P elements are those symbols that point to the subject's imagined material and S elements are effects of the unconscious speaking to the subject.
Subtractions - unnameable and unimaginable
Removing the P elements from the imagined set leaves there only the elements that do not point to any further images. Likewise, removing set S from the unconscious set leaves only the elements that are not pointed to by anything. I call those remnant sets unnamable and unimaginable.
The unnameable is the locus of Lacanian fundamental fantasy, whereas the unimaginable is the locus of the phallus, the master signifier.
It is possible that the phallus Φ points to the fundamental fantasy φ:
The preceding definitions and discussion of the poetic and symbolic is highly speculative and attractive only because of our interest in placing these concepts within the framework. Likewise the position of the phallus and the fundamental fantasy is a speculative leap upon which further reflection is called for to be followed almost surely by a reformulation. These attractive definitions are intended to mark the point where further development is desired.
Some formal development
Let us present
Lemma 1: For any A ⊂ B; A, B ⊂ Ω it holds that
It states that for A being a subset of B all images of A are also a subset of images of B. Likewise names of A are a subset of names of B. The proof is elementary.
This leads immediately to the next
Lemma 2: For any A, B ⊂ Ω it holds that
This says that images (M) of an intersection of two sets are contained in the intersection of images of each of the sets. Same holds for names (N).
Let us consider the intersection of the whole unconscious with the whole imagined and denote it by R.
It is a candidate for the Lacanian Real.
By virtue of Lemma 2 we can write for the names of R:
where the second inclusion is justified by (8) characterizing any unconscious set. The last line is justified by the fact that a subset of an intersection of two sets is also a subset of each of the sets. Same goes for the images of R:
where we used Eq. (9). We have just shown
Theorem 1:
In plain language we would say that all the images of R are imagined and all the names of R are unconscious.
Foreclosed
Let us consider a set F ⊂ Ω s.t. N(F) ⊂ F and M(F) ⊂ F. This says that all the images of F and of the names of F are contained within F. This means that F is both unconscious and imagined satisfying both (8) and (9). Then it follows that F must be a subset of both the whole unconscious and whole imagined.
We will call a set which is both imagined and unconscious a foreclosed set. A foreclosed set consists of elements that are not accessible from the outside and do not access anything outside of the set by following the signification relation. In the above we have demonstrated
Theorem 2: A foreclosed set is a subset of R - the Real.
Or,
Conscious
Let us turn to the space outside of the whole unconscious and the whole imagined. This is the domain of the conscious. Let us consider a set C in the conscious C ⊄ Υ0 ∪ Ι0. Let us take x ∈ C and y ∈ R. If x → y and y ∈ R ⊂ Υ0 we would violate the condition that nothing can point into an element of the unconscious from the outside of it. Likewise if y → x, then seeing that y ∈ R ⊂ Ι0 we would violate the condition that the imaged cannot point outside of itself. Thus we have shown
Theorem 3: For any C ⊄ Υ0 ∪ Ι0 (conscious set)
This is to say that images and names of any conscious elements are never in the Real.
Discussion
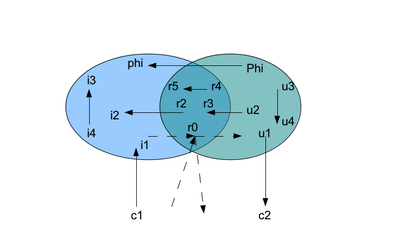
Figure C.Demonstration of possibilities for elements of Ω. See text for discussion.
Figure C produces a number of examples of signifiers/signifieds residing in various regions of Ω identified by the configuration of the whole Unconscious Υ0 and whole Imagined Ι0 and being in signification relation Σ. u3 → u4 are elements in the Unconscious. Similarly, i4 → i3 are in the Imagined. c1 points into the Imagined i2 from the Conscious space, whereas u1 in the Unconscious has a Conscious image in c2. This is all quite well expected.
The dashed lines illustrate situations that are not permitted to occur. Firstly, no elements of the Real can be images or names of any elements of the Conscious. This is the consequence of Theorem 3. Secondly, elements of the Real cannot have images in the non-Imagined Unconscious and elements of the Real cannot have names in the non-Unconscious Imagined. This is a consequence of the definition of the Imagined and Unconscious given in (10-11).
In psychoanalytic terms one might say that we have identified and rigorously characterized a privileged region of the subjective.
How are then elements of the Real reachable? They can be reached as images of the Unconscious (u2 → r3) or they can be names of the Imagined (r2 → i2). Also two elements of the Real can be in relation. The example in the figure is the pair r4 → r5. This pair may be a part of a foreclosed set. The figure suggests that if we supposed that it lists all the pairs that constitute the given signification relation Σ. However, if that were the case the pairs u3 → u4 as well as i4 → i3 - ought to be placed in the Real as they would be both isolated as unconscious and imagined.
Finally, in the strict Unconscious I speculatively placed the signifier of the Phallus Φ. It is meant to be actually in the unimaginable portion of the Unconscious - Υ0 - M(Υ0). This idea corresponds to the Lacanian view that the phallus is the master signifier which is not available to the subject. Likewise I decided the place the fundamental fantasy φ in the strict Imagined postulating above in the text that it is part of the unnamable Ι0 - N(Ι0). The Phallus signifier pointing to the fundamental fantasy is just a possibility.
Conclusion
Following the premise of the subject as being constituted by a system of signifiers I was able to show, with the aid of additional definitions, the possibility of existence of the unconscious and imagined as specific regions of the psyche. This in turn allowed me to propose a definition of set R, that may correspond to the Lacanian Real. The conscious part of the psyche is merely a leftover region that belongs to neither the unconscious not imagined. In a way the structure resembles Lacanian Schema L where the unconscious and imaginary operations intersect to produce a barred subject confronting the object of desire.
Among other constructs that seem particularly productive is the one of the foreclosed set. Also, the concepts of names and images of set A - N(A) and M(A) - respectively, seem well aimed and able to facilitate further intuitions. Nevertheless, Lacanian concepts of ego, object of desire, jouissance and subject barred are not clearly visible on the horizon, but I hope that future insights will reveal them in this or derived framework. Further work will also be needed to uncover the locus of the Lacanian Symbolic, Imaginary and Real. It would be also very productive to see how a diachronic view of evolution of the system of signifiers through time can be studied showing the processes of speech, expression and approach to the object of desire.
April 10, 2012


